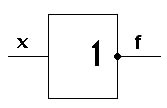
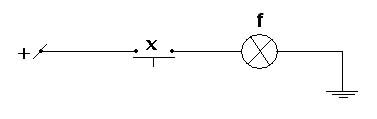
Логические основы ЭВМ.

В 1854 г. Джон Буль положил начало математической логике. Около 30 лет назад оформилась в самостоятельную дисциплину.

Математическая логика изучает только рассуждения со строго определенными объектами и суждениями, для которых возможно однозначно решить «истины» они, или «ложны». Большинство устройств ЭВМ состоит из компонентов с двумя устойчивыми состояниями и их удобно описывать на наборе логических функций принимающих значения { 0; 1 }.

Логические функции характеризуются таблицами истинности.

1)           Инверсия (логическое отрицание).

Соответствующие выражения языка:

·         Не «х»

·         неверно, что «х»

           _

 f (x) = x

Построим таблицу истинности для инверсии. Изобразим прямоугольником множество всех значений. Круг будет содержать значения множества А (значит все что входит в прямоугольник, но не входит в круг будет множеством не А). Будем «бросать» точку в прямоугольник с множествами. Результаты попадания во множество А и не А внесем в левую таблицу. В правой таблице заменим попадание во множество А на х, попадание во множество не А на f,  «нет» на 0, «да» на 1. Правая таблица и есть таблица истинности для инверсии.

В ЭВМ операция инверсии физически реализуется стандартным логическим элементом «не» – инвертором.

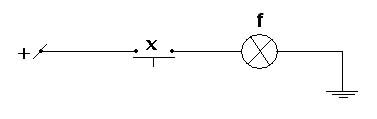
2)           Дизъюнкция (логическое сложение).

Соответствующие выражения языка:

·         Х или Y

·         Х или Y или оба                                           

 f (x,у) = x Ú у

Построим таблицу истинности для дизъюнкции. Изобразим прямоугольником множество всех значений. Первый круг будет содержать значения множества А, второй круг значения множества В. Множеством А или В будет объединение этих кругов (на рисунке закрашена серым цветом). Будем «бросать» точку в прямоугольник с множествами. Результаты попадания во множество А, В и А или В внесем в левую таблицу. В правой таблице заменим попадание во множество А на х, В на у, попадание во множество А или В на f,  «нет» на 0, «да» на 1. Правая таблица и есть таблица истинности для  дизъюнкции.

В ЭВМ операция дизъюнкции физически реализуется стандартным логическим элементом «или» - дизъюнктером.

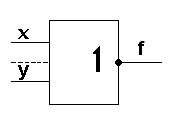
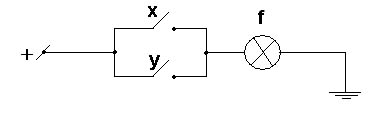
    3)           Конъюнкция (логическое умножение).

Соответствующие выражения языка:

·         Х и Y

·         Х вместе с Y

·         Х несмотря на Y

·         Х в то время, как Y

·         как Х так и Y                                           

 f (x,у) = x & у

Построим таблицу истинности для конъюнкции. Изобразим прямоугольником множество всех значений. Первый круг будет содержать значения множества А, второй круг значения множества В. Множеством А и В будет пересечение этих кругов (на рисунке закрашена темно-серым цветом). Будем «бросать» точку в прямоугольник с множествами. Результаты попадания в множество А, В и А и В внесем в левую таблицу. В правой таблице заменим попадание во множество А на х, В на у, попадание во множество А и В на f,  «нет» на 0, «да» на 1. Правая таблица и есть таблица истинности для  конъюнкции.

В ЭВМ операция конъюнкции физически реализуется стандартным логическим элементом «и» - конъюнктером.

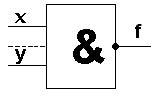
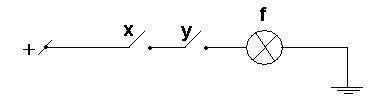
 Реализуя первые три операции, можем построить любое устройство компьютера. Прежде, чем изучать последние две операции рассмотрим тему:

4)           Импликация (логическое следование).

Соответствующие выражения языка:

·         Х имплицирует Y

·         Если Х, то Y

·         Х достаточно для Y

·         Y следует из Х

·         Y необходимо для Х

·         Y тогда, когда Х                                            

 f (x) = x ® у

Построим таблицу истинности, для импликации используя выражение – не может из «истины» следовать «ложь».

В ЭВМ нет логического элемента, который реализует операцию импликации. Для реализации данной операции строиться комбиноторно - логическая схема. На основании таблицы истинности составляется булева функция (СДНФ – совершенная дизъюнктивная нормальная форма ). 

Выписываем те строчки, где имеются 1 на выходе. Для всех таких наборов переменных запишем конъюнкции, инвертируя те переменные, которым соответствуют 0. Объединим полученные конъюнкции знаком дизъюнкции.

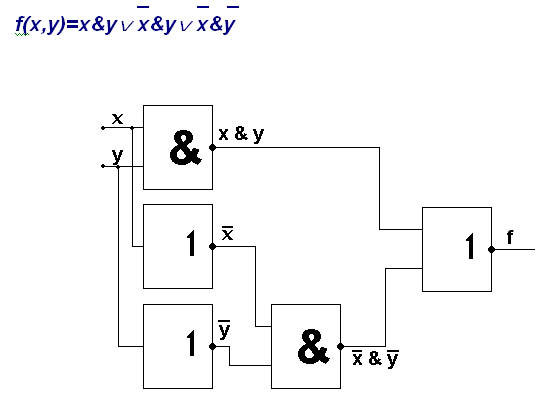
    Анализируя, видим, что схема сложна и возникает желание упростить ее. Упрощение двоичных функций называется минимизацией.

 Будем упрощать аналитически, используя закон логического склеивания.

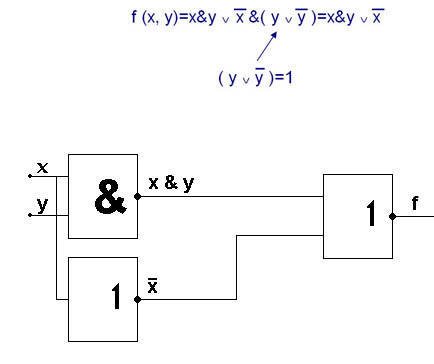
5)           Эквивалентность (логическая равнозначность ).

Соответствующие выражения языка:

·         Х эквивалентно Y

·         Х необходимо и достаточно для Y

·         Х тогда и только тогда, когда Y

·         Х если и только Y

·         Х такое же, как и Y                                           

 f (x) = x ~ у

Построим таблицу истинности,  подставляя в значения  эквивалентности «Да», если А и В принимают одинаковые значения и «Нет» в случае различных А и В.

В ЭВМ нет логического элемента, который реализует операцию эквивалентности. Для реализации данной операции строиться комбинаторно - логическая схема. На основании таблицы истинности составляется булева функция (СДНФ – совершенная дизъюнктивная нормальная форма ). 

Выписываем те строчки, где имеются 1 на выходе. Для всех таких наборов переменных запишем конъюнкции, инвертируя те переменные, которым соответствуют 0. Объединим полученные конъюнкции знаком дизъюнкции.

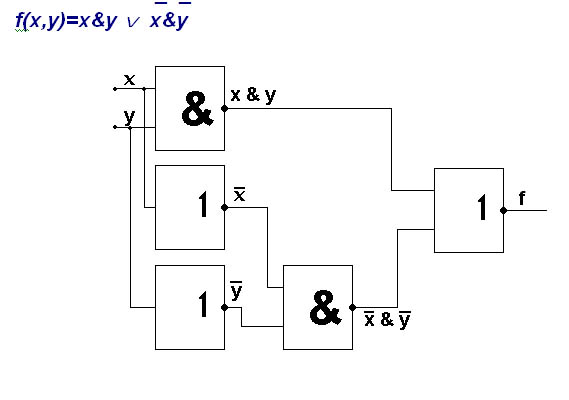
Минимизацию двоичной функции произведем на основании закона де Моргана.

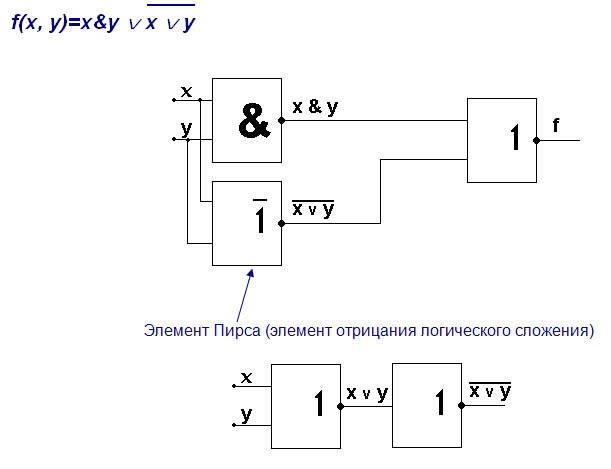
6)           Построение одноразрядного двоичного сумматора.

     p = f(x, y) = x&y

                             __                  __

z = f(x, y) = x&y Ú x&y

Минимизировать z не представляется возможным, для представления z используют совершенную конъюнктивную нормальную форму (СКНФ).

Для всех наборов переменных, для которых  функция  равна нулю,  записать  дизъюнкции,   инвертируя   те  переменные, которым соответствуют  единичные  значения,  затем   соединить дизъюнкции знаком конъюнкции.

                                               __    __

z = f(x,y) = (x Ú y)&(x Ú y)

Для дальнейшего упрощения воспользуемся законом де Моргана:

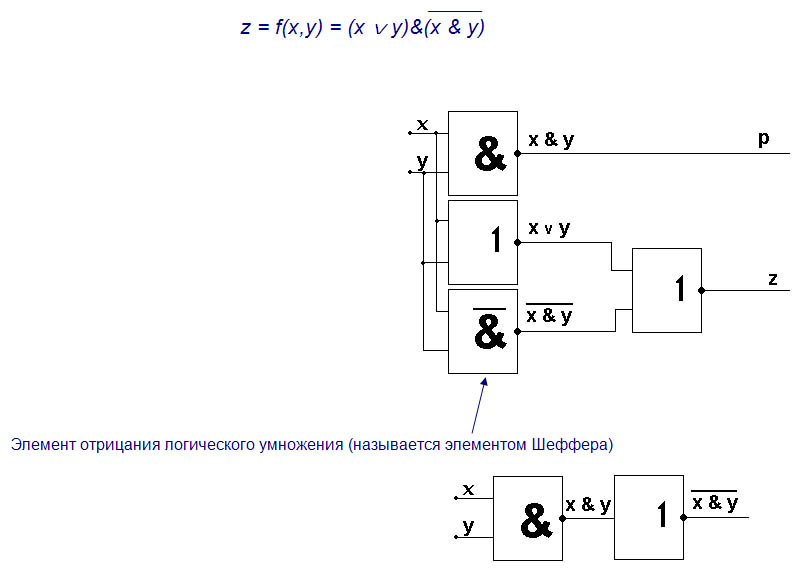
 Решение логических (содержательных) задач

Одним из разделов логики является алгебра высказываний.

Высказывание – это предложение, о котором однозначно можно сказать истинно оно или ложно. Бывают простые и сложные (составные).

Основная задача – на основании истинности или ложности простых высказываний определить истинность и ложность составных высказываний.

Составление высказываний

Пример 1:   Я поеду в Москву и если встречу там друзей, то интересно проведем время.

Решение:          М – я поеду в Москву

                            В – я встречу там друзей                                                                М×( В ® И )

                            И – мы интересно проведем там время

 Пример2:   Если я поеду в Москву и встречу там друзей, то интересно проведем время.
 Решение:                                                                                                                           М×В ® И

 Пример 3:   Не верно, что если дует ветер, то солнце светит только тогда, когда нет дождя.

Решение:          В – дует ветер

                            Д – идет дождь                                                                               

                            С – светит солнце         

Пример 4:    Если будет солнечная погода, то ребята пойдут в лес, а (и ) если пасмурная , то - в кино.

Решение:          Л – лес

                            П – солнечная погода                                                                  

                            К – кино

 Пример 5:    Не верно, что если погода пасмурная, то дождь идет тогда и только тогда, когда нет  ветра.

Решение:          Д – идет дождь

                            П – пасмурная погода                                                                           

                            В – дует ветер

Решение логических задач

I способ – с помощью таблиц истинности

 Пример 6:   Компьютер вышел из строя (нет изображения на экране монитора), однако неизвестно какое устройство не работает (монитор, видеокарта или оперативная память). Можно предположить следующее:

1)    если монитор исправен или видео карта несправна, то оперативная память неисправна;

2)    если монитор исправен, то оперативная память исправна.

Исправен ли монитор?

Решение:

1.    рассмотрим простые высказывания:

М = Монитор неисправен

В = Видеокарта неисправна

О = Оперативная память неисправна

2.    Запишем на языке алгебры логики наши предположения: 

3.    Пусть F(М,В,О) =

4.    Решить данную задачу – значит :

-        составить таблицу истинности

-        указать, при каких значениях М полученное сложное высказывание истинно.

Необходимо проанализировать все строки таблицы истинности, где F=1.

5.    Составим для данного высказывания таблицу истинности:   (самостоятельно)

Анализ таблицы показывает, что сложное высказывание истинно во всех случаях, когда М – истинно, т.е. вероятнее всего неисправен именно монитор.

II способ – с помощью преобразования логических выражений

Пример 7:   Виктор,  Роман, Леонид и Сергей заняли на математической олимпиаде четыре первых места. Когда их спросили о распределении мест, они дали три таких ответа:

1)    Сергей – первый или Роман – второй

2)    Сергей – второй или Виктор – третий

3)    Леонид – второй или Виктор – четвертый.

Известно, что в каждом ответе только одно утверждение истинно.

Как распределились места?

Решение:

Рассмотрим простые высказывания

     S1 = Сергей занял первое место

     R2 = Роман занял второе место

     S2 = Сергей занял второе место

     V3 = Виктор занял третье место

     L2 = Леонид занял второе место

     V4 = Виктор занял четвертое место

На языке алгебры логики ответы ребят можно записать следующим образом:

Конъюнкция истинных высказываний истинна. Следовательно, имеет место равенство:

Раскрыв скобки и упростив это равенство   (выполнить самостоятельно), получим:

 Другими словами, места на олимпиаде распределились так:

    Сергей  - 1 место;  Леонид – 2 место;  Виктор – 3 место;  Роман – 4 место.

В МЕНЮ